Glossar
Obertonreihe
In jedem Ton, der klingt, schwingt eine ganze Serie anderer Töne mit. Töne in der Musik sind eigentlich bereits Klänge, die ein breites Frequenzspektrum umfassen.
Wenn man eine Saite anschlägt, beginnt sie zu schwingen, wodurch sich die Luft um sie in Schallwellen ausbreitet: dadurch wird sie hörbar. Nun ist dieses Schwingen nicht nur ein Hin und Her auf der gesamten Länge der Saite – es bilden sich Oberschwingungen, und zwar überall dort, wo die Saitenlänge sich in gleiche Teile zerlegen läßt: bei der Hälfte der Saite (dort überaus deutlich wahrnehmbar), dem Drittel, dem Viertel etc. (mit stetig abnehmender Lautstärke).

Bei der Teilung einer Saite in gradzahlige Verhältnisse ergeben sich die grundlegenden Intervalle. Die Halbierung der Saitenlänge ergibt die Oktave, einem Drittel entspricht die Quinte, eine Viertelung bringt erneut eine Oktave, etc.
Diese Verhältnisse findet man auch im einzelnen klingenden Ton wieder; sie ergeben die Obertonreihe:

Auf (1) findet sich der Grundton; (2), (4), (8) und (16) sind die Oktaven darüber; (3), (6) und (12) sind die Quinten. Die übrigen Obertöne sind nicht mehr ohne weiteres in das Modell der Musik des Abendlands unterzubringen, das eine Oktave in zwölf gleichförmige Intervalle zerteilt – die Notation führt ein wenig in die Irre, weil alle anderen Töne im Obertonspektrum ein wenig höher oder tiefer erscheinen, als wenn man sie, wie notiert, auf dem Klavier spielt.
Weiterführende Anmerkungen:
- Das Prinzip der „schwingenden Saite” findet bei Blasinstrumenten im Schwingen der Luftsäule im Inneren der Instrumente ihre Entsprechung, bei der menschlichen Stimme im Schwingen der Stimmbänder.
- Eine einzelne Schwingung (ohne jeden Oberton) läßt sich nur auf elektronischem Wege erzeugen; tatsächlich ist die sog. Sinusschwingung Ausgangspunkt in der Klangerzeugung zahlreicher Synthesizer.
- Die unterschiedliche Stärke und Ausprägung der erklingenden Obertöne ist – maßgeblich, aber nicht ausschließlich – für die Klangfarbe verantwortlich, an der man unterschiedliche Instrumente voneinander unterscheiden kann.
- Selbst die Quinte – immerhin erst Oberton (3) – ist in der Teilung der Oktave in zwölf gleichförmige Schritte („Halbtöne” => wohltemperierte Stimmung) nicht „rein” darstellbar: man nimmt hier eine minimale Abweichung vom 2:3-Verhältnis in Kauf. Allein dies hat außerordentlich weitreichende Konsequenzen. – Noch krasser tritt diese Abweichung zutage, je weiter man sich in die komplexeren Verhältnisse begibt: 4:5 (Oberton 5) etwa ist schon derart weit entfernt von seiner Entsprechung im wohltemperierten Gefüge, daß die Behauptung, der Dur-Dreiklang (wie er in (4)-(5)-(6) ja notiert erscheint) sei naturgegeben, weil er in der Obertonreihe in jedem Ton mitschwingt, fast schon zur Belustigung Anlaß gibt.
Temperierte Stimmung
Im Eintrag zur Obertonreihe hatte ich angedeutet, daß man aus dem Erscheinen des Durdreiklangs auf den Obertönen 4-6 nicht auf dessen Naturgegebenheit schließen kann. Ich will das etwas näher ausführen.

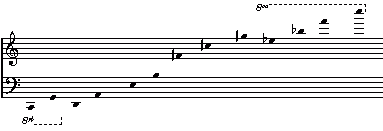
Wenn man, ausgehend vom Kontra-C, sieben Oktavschritte nach oben geht, landet man beim fünf-gestrichenen C. Eben dort kommt man auch nach zwölf Quintschritten an. Problemlos funktioniert dies jedoch nur in der Notenschrift oder auf einem Klavier.
Oktaven haben ein Frequenzverhältnis von 1:2; wenn das »Kontra-C« 60Hz hat, liegt das »C« bei 120Hz. Die Rechnung lautet: 60 * 27 – man landet nach sieben Oktaven bei 7680Hz. - Die Frequenzen zwischen Quinten liegen im Verhältnis 2:3; wenn man wieder bei 60Hz startet, ist das nächste G bei 90Hz, das D bei 135Hz, das A bei 202,5Hz – und man merkt jetzt schon, daß man ganz oben keineswegs bei einer gradzahligen Zahl ankommt, es ergeben sich 7784,8Hz (60 * (3 / 2)12).
Die Differenz zwischen diesen beiden Werten nennt man das pythagoreische Komma, und sie hat weitreichende Konsequenzen für das System der Musik des Abendlands, das auf einer Zwölfteilung der Oktave basiert. Man muß sich, wenn man ein Tasteninstrument stimmen will, entscheiden:
- Entweder, die Quinten in bestimmten Tonarten sind rein und wirklich im Verhältnis von 2:3 gestimmt. In diesem Fall sind andere Tonarten aber unbenutzbar, weil stark verstimmt.
- Oder man teilt die Oktave in zwölf Töne mit jeweils gleichem Abstand. Dann kann man sämtliche Tonarten verwenden, hat es aber nicht mehr mit reinen Quinten zu tun.
Wenn man alte Kirchenorgeln hört, die anfällige Restaurierungen in ihrer originalen Stimmung belassen haben, kann man noch heute eine Reihe von Experimenten finden, mit denen man einst einen Kompromiß zwischen reiner Stimmung und der Verwendung möglichst vieler Tonarten gesucht hat. Erst mit der Durchsetzung der zweiten Alternative, der temperierten Stimmung, wurde die Musik von J.S.Bach und seinen Nachfolgern möglich, die wesentlich darauf beruht, die Chromatik der Halbtöne in vollem Umfang zu nutzen. Tatsächlich ist es nicht zuletzt Bach selber zu verdanken, daß die temperierte Stimmung als „wohltemperiert” gilt: sein „Wohltemperierte Klavier” mit ihren 2*12 Inventionen und Fugen in allen zwölf Dur- wie Molltonarten ist Bachs Parteinahme in einem Streit, der erst zu seinen Lebzeiten entschieden wurde.
Man hat es hier mit einem höchst artifiziellen System zu tun, das in die Ebene des Klangs eingreift – die sinnlich erfahrbare Ebene von Musik wird der Verfügung des Verstandes unterworfen; die Ratio übernimmt auf einer Ebene, von der man vermuten würde, daß sie ihm eigentlich unzugänglich ist.
Dabei darf man allerdings nicht vergessen, daß alle Streich- und Blasinstrumente tendenziell immer noch in der Lage sind, nicht-temperierte Akkorde zu spielen – solange kein Tasteninstrument[1] in der Nähe ist, tun sie das auch regelmäßig. Besonders deutlich wird das, wenn tiefe Instrumente mit relativ wenigen Obertönen reine Durakkorde spielen. Ich denke da an diverse Passagen von drei oder vier F-Hörnern bei Wagner und Bruckner, oder an das Ende von Mahlers 6. Sinfonie – wenn dort die tiefen Posaunen nach viel A-Moll noch kurz nach Dur wechseln, schaukelt sich ein Klang auf, der doppelt so laut zu sein scheint wie die Akkorde zuvor.
- [1] Oder auch ein Saiteninstrument mit Bünden - aber das ist noch eine eigene Thematik.
Nachtrag: Die Oktave über der Basis von 60Hz hat 120Hz, die (reine) Quinte 90Hz. Für die temperierte Stimmung gilt die Formel:
Dabei ist »fbase« die Basis, und »i« der gesuchte Halbton (1-12). Über 60Hz ergibt der 7.Halbton (die Quinte) dann 89,899 Hz. Das ist eine denkbar kleine Abweichung vom Ideal, von der man meinen könnte, daß man sie nicht hören kann. Man muß aber bedenken, daß die beiden Töne, die in diesem Intervall gemeinsam klingen, ihrerseits Obertöne haben, die gerade bei tiefen Instrumenten in Bereichen liegen, die deutlich hörbar sind - und die Dissonanzen gerade im hohen Frequenzband wirken überaus scharf und unangenehm.
Nachtrag 2: In der Wikipedia findet sich eine Tabelle für die Umrechnung der Abweichung von temperierter und nicht-temperierter Stimmung in Cent-Werte, wie sie bei der Programmierung von Tunings in Synthesizern verwendet werden - wenn man ein Gerät besitzt, das selbst-programmierte Tunings unterstützt, kann man sich für eigene Experimente daran orientieren.
Kombinationstöne
Wenn zwei Töne gleichzeitig erklingen, entsteht ein dritter Ton – eine Kombination aus den „Pattern” der beiden Töne –, der sich aus den Frequenzen der beiden Töne bildet[1]. Wenn z.B. der erste Ton in 120Hz (120 mal pro Sekunde) schwingt, der zweite in 180Hz (180 mal/Sekunde), „treffen” sich die Amplituden im gemeinsamen Vielfachen bei 60Hz (60 mal/Sekunde). Diese „Peaks” bilden eine Frequenz, in diesem Fall einen Ton im hörbaren Bereich: eine Kombination der beiden Ausgangstöne, einen „Kombinationston”, oder (wobei ich den Begriff eher unpassend finde) „Unterton”.
Die Frequenzen im Beispiel sind eine (reine, d.h. nicht-temperierte) Quinte im Frequenzverhältnis 2:3. Der Kombinationston liegt eine Oktave unter dem Grundton.
Das, was hier im Bereich von „Sound” passiert, ist exakt dasselbe, was man in der Rhythmik ständig erlebt. Eine Überlagerung von einem Pattern im 2/4 trifft sich in der Polyrhythmik mit einem in 3/4 alle 6/4. Wenn der gemeinsame Puls der Pattern hinreichend übereinstimmt, etablieren die beiden Pattern ein drittes. – Dasselbe passiert, wenn zwei Töne aufeinander treffen, die in ihrer Klangfarbe[2] „genug” gemeinsam haben: ein dritter Ton wird hörbar.
Die Formel[3,4] zur Berechnung der Frequenz eines Kombinationstons (ffreq) zu der Frequenz eines Basistons (fgt) in Relation zu dem Verhältnis der Frequenz der Basis (vgt) zu der des höheren Tons (vi) ist simpel:
Gewöhnlich sind Kombinationstöne so leise und/oder so tief, so daß sie nicht wahrgenommen werden. Dabei können Kombinationstöne auch außerhalb des Hörbereichs menschlicher Ohren zu einem Problem werden, z.B. in der Audiotechnik, dort z.B. bei der Wandlung von analogen in digitale Signale.
Es gibt Situationen, wo Kombinationstöne hörbar werden, was man sich zu nutze machen kann, oder wo das stört:
- [1] Ich kenne das Phänomen, solange ich Geige spiele, hatte bisher aber keine Erklärung dafür. Die Lösung des Rätsels kommt von Gregory Bateson, Mind and Nature, Hampton Press 2002, Pg.74f.
- [2] Bei phasengenauen Sinuswellen lassen sich Kombinationstöne leicht herleiten (es sollte möglich sein, auch deren Lautstärke mathematisch zu beschreiben). Bei Tönen von akustischen Instrumenten – die ja selber schon Klänge sind, wenn man das Obertonspektrum einbezieht – sieht dies deutlich komplexer aus.
- [3] Ich habe dafür keine Herleitung im 'net finden können; sie ist aber einfach genug.
- [4]
Kombinationston in einer Quinte (Frequenzverhältnis: 2:3, wie im Beispiel am Anfang):
➔ eine Oktaven unter dem Grundton.
Kombinationston in einer (reinen) großen Terz (Frequenzverhältnis: 4:5):
➔ zwei Oktaven unter dem Grundton.
Kombinationston in einer (reinen) kleinen Terz (Frequenzverhältnis: 5:6):
➔ zwei Oktaven + Quinte unter dem Grundton. - [5] Man kann auf einer Gitarre im High-Gain Terzen spielen, indem man eine der Saiten so zieht, daß die temperierte zu einer nicht-temperierten Terz wird. Wie man das macht, bleibt mein Betriebsgeheimnis...
Sonatenhauptsatz
Der Begriff „Sonatenhauptsatz” bezeichnet eine musikalische Form, deren Bauplan, seit Haydn, dem ersten Satz einer Sonate oder Sinfonie zugrunde liegt.
Sie beginnt mit einer Exposition, die sich aus einem Haupt- und einem Seitenthema zusammensetzt. Das Hauptthema wird in der Ursprungstonart vorgestellt; nach einer modulierenden Überleitung erscheint das Seitenthema in einer anderen, kontrastierenden Tonart [1]. In dieser zweiten Tonart endet die Exposition; idR wird sie wiederholt.
Darauf folgt die Durchführung, in der die beiden Themen variiert und entwickelt werden, wobei neben den beiden ursprünglichen Tonarten auch entferntere tonale Zentren angesteuert werden.
Schließlich folgt die Reprise, in der die beiden Themen wiederholt werden. Dabei erscheint jedoch das Nebenthema in der Haupttonart.

Ich möchte zwei Aspekte herausheben, die m.E. zentral sind:
- Man findet hier ein Modell, mit dem sich auch groß angelegte Formverläufe organisieren lassen. - Die Exposition schließt in einer Nebentonart, und damit in einer Spannung, von der der Hörer eine Auflösung erwartet. Die Durchführung überhöht noch diesen Konflikt zwischen den unterschiedlichen tonalen Zentren, weil in ihr in immer entferntere Tonarten moduliert wird. Erst in der Reprise löst sich die Spannung, wenn endlich die beiden tragenden Themen im gleichen tonalen „Kraftfeld” erscheinen.
- Neben dem Potential, längeren Zeitverläufen die nötige architektonische Statik zu verleihen, findet sich eine Akzentverlagerung weg von der Wiederholung des musikalischen Materials hin zu dessen thematischer Entwicklung. Frühere Tanzformen werden durch die „wörtliche” Wiederholung kompletter formaler Abschnitte organisiert. In der Sonatenform hingegen gewinnt das verändernde Spiel mit dem Ausgangsmaterial immer mehr an Bedeutung. Dies geschieht - zum einen - durch die Versetzung des Seitenthemas in der Reprise in eine andere Tonart; zum anderen gewinnt die Rolle der Durchführung eine immer größere Bedeutung, bis schließlich - schon bei Brahms - nahezu alles nur noch Durchführung ist, d.h. verändernde und entwickelnde Variation.
Es würde zu weit führen, in die Darstellung der Geschichte der Sonatenform einzusteigen. Anzumerken bleibt, daß sie erstmals Mitte des 18.Jh in den Sinfonien und Streichquartetten Joseph Haydns erscheint, und bis in die Musik unserer Tage eine wichtige Rolle spielt.
Das beschriebene Modell findet sich in Reinform nur in der Wiener Klassik, und selbst dort bereits durch formale Experimente variiert. In der Folge erweist sich die Sonatenform als unerhört robust für alle möglichen Erweiterungen und Veränderungen. So wird der harmonische Rahmen immer weiter gefaßt - die Tonarten für das Seitenthema entfernen sich immer weiter von der Ursprungstonart; es gibt formale Erweiterungen wie ein zunehmendes Gewicht für die Einleitung bzw. Coda; es gibt auch ein drittes Thema; Versuche, das usprüngliche Modell über mehrere Sätze zu verteilen; uvm.)
- [1] In der „Urform” findet man das Seitenthema auf der vierten Stufe der Haupttonart (wenn diese in Dur ist) bzw. in der parallelen Durtonart (wenn die Haupttonart in Moll steht).
Tristan-Akkord
Dies ist eine der berühmtesten Sequenzen der Musikgeschichte:

Klangzitat (Daniel Barenboim / Berliner Philharmoniker):
Der Pfeil markiert den sog. Tristan-Akkord – ein Konstrukt, das die Musikwissenschaften seit 1865 immer wieder beschäftigt hat[1]. Es gehört(e) zum guten Ton für jeden Musiktheoretiker, eine eigene Meinung zur Funktion dieses Akkords für den Zusammenhang zu haben, und zwar am besten eine, die kein anderer zuvor vertrat. Die Glaubensstreitigkeiten in diesem Fall haben sich verflüchtigt; die Wikipedia gibt den Stand der Dinge recht gut wieder. – Der entscheidende Punkt ist aber, daß man an dieser Stelle eine Debatte mit einigem Recht überhaupt führen kann.
Die Harmonik hatte sich bis zu diesem Punkt in der Musikgeschichte zur Funktionsharmonik entwickelt, in der genau eine Tonart im Zentrum einer Komposition steht, die von allen anderen Tonarten gewissermaßen umkreist wird. In C-Dur ist G-Dur die Dominante, F-Dur die Subdominante; in der Folge aus F-G-C definiert sich die C-Dur-Kadenz. Die übrigen Dreiklänge, die sich aus den Tönen der C-Dur-Tonleiter bilden lassen, können als Stellvertreter für die drei Kadenzakkorde dienen. Drei- oder gar Vierklänge, die Töne enthalten, die nicht in C-Dur vorkommen, haben noch entferntere Verwandschaftsverhälnisse zur Ausgangstonart, sind aber immer hierarchisch auf sie bezogen. – Ohne das an dieser Stelle ausufern zu lassen: entscheidend ist, daß jeder Akkord eine eindeutige (well: schon hier mindestens zweideutige) Funktion hat. Alle harmonische Entwicklung gewinnt ihre Spannung aus der Gravitation im Abstand zur Haupttonart.
Im Tristan-Akkord findet sich das erste Beispiel einer Harmonik, die mehrdeutig (besser: vieldeutig) ist – man kann von hier in verschiedene Richtungen weiter gehen; Schönbergs Analyse spricht von „vagierenden” Akkorden, die in ihrer Vieldeutigkeit als Schaltstelle für überraschende harmonische Sprünge dienen können.
So bezieht sich der Tristan-Akkord auf die Dominante von a-moll, „löst” sogar sich scheinbar in sie „auf”, so daß er den Charakter einer Zwischendominante bekommt (tatsächlich gibt es im Verlauf der Oper einige Stellen, wo die Sequenz nach a-moll bzw. A-Dur weitergeführt wird). Ebenso könnte man ihn aber auch – wenn man „dis” und „gis” enharmonisch nach „es” und „as” verwechseln darf, und das kann man hier zweifellos tun - als zweite Stufe (Stellvertreter der Subdominante) in Es-Moll deuten (was nur Theorie ist – zumindest was den „Tristan” betrifft). Dann könnte es sich aber auch um ein Konstrukt handeln, das sich wirklich jeder funktionsharmonischen Deutung entzieht, nämlich – ich weiß, das klingt jetzt etwas ausgeklinkt – um die Dominante der Vermollung der Subdominante mit hochalterierter Terz. Genau so erscheint der Akkord dann aber auch, und zwar ausgerechnet in den allerletzen Takten der Oper, nach ca. vier Stunden, für die finale Schlußwirkung – die sich dann sogar einstellt (E-Dur mit kleiner Septe geht nach H-Dur).
- [1] Ich kann mir den Hinweis auf das Notat dieser Stelle durch die zukünftige Leiterin Bayreuths nicht verkneifen.
Zwölftontechnik / Dodekaphonie
Unter »Zwölftontechnik« oder »Dodekaphonie« versteht man die Methode der Komposition mit „zwölf nur aufeinander bezogenen Tönen” (Schönberg). Das Material, mit dem komponiert wird, ist nicht mehr die Funktionsharmonik der tonalen Ordnung, sondern eine vom Komponisten vorher festgelegte Folge von allen zwölf Tönen der chromatischen Tonleiter.
Eine »Reihe« besteht aus genau zwölf Tönen, wobei sich kein Ton - unabhängig von seiner Lage: ein »C« z.B. gilt in allen Oktaven als derselbe Ton - wiederholen darf. Dabei lassen sich insgesamt 48 Varianten verwenden: neben der »Grundform« der »Krebs« (Spiegelung um die vertikale Achse - die Grundform wird von hinten nach vorne gespielt), die »Umkehrung« (Spiegelung um die horizontale Achse - alle Intervallverhältnisse erscheinen umgedreht), der »Krebs der Umkehrung« (Spiegelung um beide Achsen), sowie die Transposition dieser vier Varianten auf alle zwölf Stufen der chromatischen Tonleiter.
Beispiel: die vier Varianten der Reihe, die Alban Bergs Violinkonzert zugrunde liegt (man kann die Symmetrien auch dann erkennen, wenn man keine Noten lesen kann).
Grundform
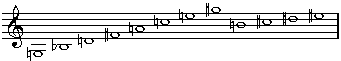
Krebs
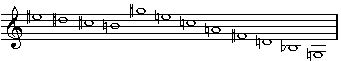
Umkehrung
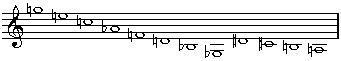
Krebs der Umkehrung
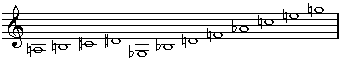
Alle Töne einer Reihe müssen stets vollständig und in der vorgegebenen Reihenfolge verwendet werden; zuerst hatte Schönberg sogar verboten, einzelne Töne in unmittelbarer Folge zu wiederholen. Dabei wird die Reihe sowohl zur vertikalen wie auch horizontalen Organisation verwendet: sie bildet die Melodien wie auch die Akkorde, wobei alle Mischformen erlaubt sind (z.B. können ihre ersten vier Töne einen Akkord bilden, über dem die restlichen acht Töne als Melodie geführt werden). Die Reihe und ihre Varianten können auch parallel zueinander erscheinen - sie können also polyphon ineinander verschachtelt werden.
- Das erste Zwölftonwerk im strengen Sinn ist Schönbergs Klaviersuite op.25 von 1921.
- Der Sinn dieses Verfahrens liegt darin, mit jedem tonalen Zentrum gründlich zu brechen. Wenn jeder der zwölf Töne gleich häufig auftritt, gibt es keinen Ton mehr, der einen Schwerpunkt darstellen und eine „Schwerkraft” entwickeln oder etwas wie eine vorherrschende Tonart - Tonalität - etablieren könnte.
- Das Verfahren ist alles andere als eine radikale Neuorientierung, die Schönberg sich am grünen Tisch ausgedacht hätte. Seit Wagner - ja, seit Beethoven - tendiert das harmonische Geschehen immer mehr dazu, das tonale Zentrum zu verschleiern und ins Ungewisse zu ziehen. Die erste Sinfonie Beethovens beginnt mit einem Dominantakkord (ein Skandal für das Musikleben im Wien des ausgehenden 18.Jh) und stellt damit das tonale Zentrum wohl noch ins Zentrum, aber eben schon nicht mehr an den Anfang. Wagner treibt es im Tristan soweit, daß die A-Moll-Tonika im Vorspiel zwar immer wieder angesteuert, aber nie tatsächlich erreicht wird. Schönberg zieht - nach etlichen Experimenten, die nach seinem (äußerst beachtlichen) spätromantischen Frühwerk zuerst in ein Stadium freier Atonalität führen - hier lediglich die Konsequenzen.
- Die Musik Schönbergs und seiner Schüler ist alles andere als deterministisch - dies ist erst die serielle Musik der Nachkriegszeit. Wenn man etwa eine Aufführung von »Moses und Aaron« erlebt hat, fällt es schwer zu glauben, daß diese komplexe, höchst farbige Oper auf der Verwendung genau einer Zwölftonreihe basiert.
- Das Wort von der „Atonalität” ist ein Kampfbegriff, der Zwölftonmusik letztlich als „Unnatur” diffamieren will. Man muß verstehen, daß auch die tonale Ordnung der Kadenz alles andere als natürlich ist, sondern eine äußerst artifizielle Verbiegung von natürlichen Phänomen vorstellt.
- „[...] ich bin Musiker, und habe mit Atonalem nichts zu tun. [...] Atonal wird man irgendein Verhältnis von Tönen sowenig nennen können, als man ein Verhältnis von Farben als aspektral oder akomplementär bezeichnen dürfte.” (Arnold Schönberg, Harmonielehre, Universal Edition 1922 (Faksimile), S. 486.)
Serielle Musik
Unter den Begriff »Serielle Musik« oder »Serialität« fällt jene Musik, die kurz nach dem zweiten Weltkrieg entstand. In ihr werden die Ideen von Arnold Schönberg und seinen Schülern aufgegriffen und auf die Spitze getrieben. Für eine Komposition wird nicht nur die Abfolge der zwölf Töne der chromatischen Tonleiter vorher festgelegt (Zwölftonmusik), sondern auch jene aller anderen musikalischen Parameter (Lautstärken, Instrumentierung, etc.), und schließlich selbst die Beziehung zwischen all diesen Reihen. Am Ende hat der Komponist nichts weiter zu tun, als die im Vorfeld definierten Serien zu Papier zu bringen. Der kreative Prozeß beschränkt sich also auf die Erfindung (bzw. der wiederum rationalen Kriterien unterworfenen Konstruktion) der Reihengestalten - der Rest besteht aus einer automatisierbaren Befolgung dieser Regeln.
Hier findet sich - zum einen - der Niederschlag des Traumas des Krieges: die romantische Musiktradition hatte sich völlig desavouiert, hatte man doch soeben erlebt, wie leicht sie sich für die Ideologie der Nazis einspannen ließ - Wagners Opern hatten dazu beigetragen, der faschistischen Gewalt einen feierlichen Anstrich zu geben, und Liszt wurde im Radio gespielt, um die Siegesmeldungen der Wehrmacht anzukündigen. Alles, was genialisch-übermenschlich daherkam, geriet unter Generalverdacht und wurde für die Katastrophe verantwortlich gemacht[1].
Zum anderen wurde der Weg bereits in den 30ern - noch vor der Machtübernahme Hitlers - freigeräumt, die letzten Schritte zu einer vollständig durchrationalisierten Musik zu gehen. Anton Webern - ein Schüler Schönbergs - hatte ihn in seinen Versuchen, auch die Ebene der Klangfarbe in Reihen zu organisieren, letztlich längst beschritten.
- Die serielle Musik ist ein historisches Experiment, das sich als Sackgasse erweist. Dabei darf man jedoch nicht vergessen, daß es seinerzeit keine Alternative gab: sämtliche Komponisten Ende der 40er und Anfang der 50er Jahre sind Serialisten, auch solche, die später fundamental andere Wege gehen (namentlich Hans Werner Henze).
- Die Werke lassen sich hörend nicht nachvollziehen - und sind letztlich auch nicht nur annähernd präzise aufführbar. Dies haben die Komponisten (namentlich Karl-Heinz Stockhausen) früh begriffen, und deshalb bald mit elektronischem Equipment experimentiert.
- Fast zeitgleich finden Experimente (zentral hier: John Cage) mit Techniken der Aleatorik[2] statt - Musik verwandelt sich in eine Performance, und Noten werden nach dem Zufallsprinzip generiert. Dies ist insofern bemerkenswert, weil sich die Resultate des Zufalls für den Hörer letztlich nicht von denen vollständiger Determiniertheit unterscheiden. Dabei ist beiden Verfahren jedoch ein ganz grundsätzliches Element gemeinsam: sie stellen die Rolle des Individuums bei der Entstehung eines Kunstwerks grundsätzlich in Frage.
- Was nach dem zweiten Weltkrieg in der Musik stattfand, hat gewisse Parallelen zu den Entwicklungen in der bildenden Kunst nach 1918. Futurismus und Dada haben in ihren programmatischen Äußerungen mehr als nur eine äußerliche Gemeinsamkeit mit jenen in Serialität und Aleatorik [3].
- [1] Ich kann dieses Thema hier nur antippen - egal, wie ich diese Sätze formuliere, bleiben sie in ihrer Kürze letztlich falsch. Mehr - und momentan auch nur sehr unvollständig - findet sich in meinem "Wege"-Baukasten.
- [2] „Alea” - lat. Würfel: Zufall.
- [3] Bei Walter Essl findet sich ein lesenswertes Essay zu dem Thema (sofern man den dort gelegentlich sehr weit ausholenden Griff in die Kiste philosophischer Grundbegriffe ausblendet).
- Impressum
- Hosted by Manitu
- PHP-Credits
- Lizenz (CC)