Systemtheorie (Ausblick)
Ich habe am Wochenende ein wenig im Netz gestöbert und nach ersten Texten zu Niklas Luhmanns Theorie über „soziale Systeme” gesucht. In der Wikipedia bin ich über den Vater der soziologischen Systemtheorie gestolpert, Talcott Parsons. Diesen Namen habe ich bislang allenfalls aus der Ferne gehört, und kenne mich in der angelsächsischen Tradition, in der dessen Soziologie steht, auch nicht aus. Dennoch ist mir wieder eingefallen, warum mich ein solcher Theorieansatz nie interessiert hat - und womit ich das Werk Luhmanns bislang verwechselt hatte.
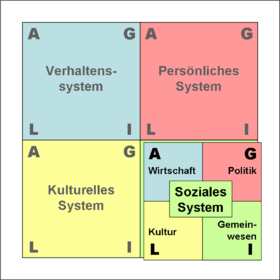
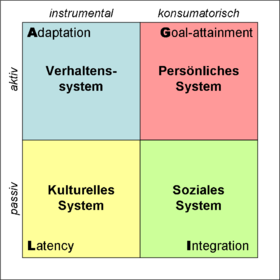
Die Grafik (Quelle: Wikipedia) illustriert Parsons' AGIL-Modell. Demnach weist ein „System” immer vier Merkmale auf, die wiederum auf unterschiedlichen Ebenen sortiert sind. Dabei besteht jede der abstrakten Ebenen des Systems wiederum aus einem System, das ebenfalls vier Ebenen aufweist.
Ich verweise auf die Wikipedia - mehr weiß ich auch nicht zu dem Thema, außer der Tatsache, daß sich bei mir sofortiger Unwille breit macht, mich mit solchen Ansätzen näher zu beschäftigen. Mit Schemata, die in einige wenige rechteckige Kästchen passen und Rekursion auf Wiederholung reduzieren[1], kann man nicht einmal ein hinlänglich komplexes Computerprogramm beschreiben, geschweige denn komplexe gesellschaftliche Zusammenhänge. - Aber das ist Parsons, nicht Luhmann.
Ich habe zwei knappe Einführungen gefunden (diese - eine echte Rarität: das Vorwort zur koreanischen Übersetzung von Luhmanns Buch - und diese, beide etwas ausführlicher und letztlich besser lesbarer als der Wikipedia-Artikel), die beide eine Begrifflichkeit andeuten, die hilfreich sein könnte. Dabei finden sich in Dirk Baeckers Vorwort zwei Anregungen für den Umgang mit dem Werk, die ich auch grundsätzlich bemerkenswert finde:
[Ein bestimmter fachlicher Zusammenhang] markiert ein weiteres Mal jene Komplexitätsschwelle der Theorie Luhmanns, an der auch wohlwollende Leser häufig scheitern. Man lasse sich davon nicht entmutigen. Nicht alles versteht man bei der ersten Lektüre. Vieles muss man überlesen, ohne es zu verstehen, um bei anderer Gelegenheit darauf zurückzukommen.
Ich muß zugeben, daß ich mit einer ganzen Reihe von Büchern so vorgegangen bin - gelegentlich sogar, um erst nach Jahren oder aber auch überhaupt nicht (manchmal trägt selbst das Früchte) auf sie zurückzukommen.
Die zweite Anregung ist nicht weniger bemerkenswert in der Formulierung von Selbstverständlichem:
Das meiste erschließt sich nur, wenn man damit zu arbeiten versucht. Das allerdings gilt für fast beliebige Gegenstände. Man muss es nur ausprobieren.
Genau das werde ich in der Folge hier versuchen.
- [1] Ich müßte ausführlicher darlegen, warum Rekursion mit Wiederholung rein gar nichts zu tun hat - ebenso wenig übrigens wie mit Dialektik -, und warum man mit einem Blick sehen kann, daß Parsons' Diagramme das eine vorgeben, aber nur letzteres bieten. Wenn ich irgendwann Lust dazu habe, hole ich das noch nach.